What is the cost-average effect in a savings plan?

Savers usually have the possibility to choose between two variants regarding the monthly payments. On the one hand, it is possible to purchase a certain number of shares (funds) or units(gold or silver bars) every month. The alternative is to buy the corresponding values at regular intervals for a certain amount of euros.

But which of these two options is more attractive for savers from a financial point of view? We would like to explain this in more detail in our article, because the so-called cost-average effect (CAE for short) comes into play.

Savings contribution with a fixed euro amount: the usual variant

The most commonly used variant, in which form the usually monthly savings contribution is determined for savings plans, is a fixed euro amount. So, as a saver, you decide, for example, to purchase the corresponding number of silver or gold bars every month for 200 euros. This form of savings contributions is also possible with the vast majority of other savings forms in addition to the precious metal savings plan, such as:

Fund savings plan
ETF savings plan
Bank savings plan
Private pension insurance
Share savings plan

With the bank savings plan or also with the private pension insurance the monthly contributions must always be made on euro basis anyway, since no shares or pieces of a value can be bought. With the precious metal savings plan, on the other hand, you have this basic choice. There you can either purchase a fixed number of bars or coins per month. Or you also decide on a certain euro amount, for which then this coins or bars are purchased.

What is the cost-average effect?

At this point, it is interesting for savers to know whether there is a difference between the two previously explained variants in terms of return. In fact, this difference exists, namely due to the so-called cost-average effect. The average cost effect originally comes from asset management. It is based on the fact that with goods or financial products that are subject to a changing price, there is always the risk that the saver buys too expensive.

To prevent this, it is advisable to divide assets or available capital among as many equally sized amounts as possible. Ideally, this should also be done over as long a period as possible. For example, if you already have capital in the amount of 10,000 euros, which you could invest in gold bars, for example, it would usually - but not always (we will come to that) - make more sense to spread the capital over 50 equal monthly installments of 200 euros each in the future, due to the cost-average effect.

For some time now, the cost-average effect has been used more and more often in connection with savings plans. After all, these are also often values or shares that are acquired on a regular basis. The cost-averaging effect is particularly evident in fund savings plans and precious metal savings plans.

How does the cost-averaging effect work in detail?

So why is it possible through the cost-average effect to buy, for example, a 1-gram gold bar at a cheaper price on average if you decide on a fixed euro amount per month? One thing first: The fact that the cost-average effect works is undisputed on a broad basis and has already been proven by numerous calculations and studies. Only the impact of the effect is sometimes somewhat overestimated, which we will discuss in more detail later in this article.

cost function

However, the fact that the average cost effect works is based on a rule that is easy to explain. For example, if you regularly purchase small gold bars as part of a precious metals savings plan, then their price will effectively change on a daily basis due to the change in the price of gold. If you have specified in your savings plan that you would like to deposit, for example, 200 euros per month and buy gold bars for it, then you will acquire proportionately more bars or fractions when prices fall than when gold prices rise.

Exactly this fact leads to the fact that you can acquire on the average for 200 euros somewhat more gold bars, than if you had specified within the savings plan to acquire for example always exactly five 1 gram bars monthly. Then you always buy the same number of gold bars, completely independent of the respective price. Optimally, the cost-average effect works in the area of the precious metal savings plan, if the purchase of bars in the form of a fractional ownership is also possible.

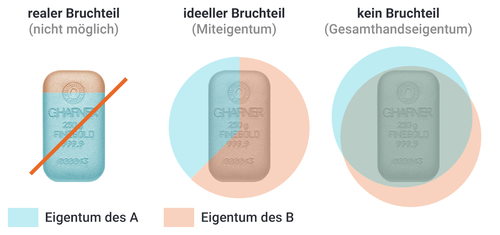
Precious metal savings plan with and without fractional ownership

We would like to illustrate the advantages of fractional ownership when buying gold or silver bars with an example. Let's assume that within the precious metal savings plan you have decided to purchase 5-gram gold bars on a regular basis. Based on the current gold price for an ounce of fine gold of around 1,520 euros, such a 5-gram gold bar would cost around 250 euros. However, since you only want to pay 200 euros per month into the savings plan, you would only be able to afford a 5-gram gold bar after two months if you can only purchase "whole" bars as part of the savings plan.

However, if it is a precious metals savings plan based on fractional ownership, you could deposit 200 euros month after month and not have to wait two months to afford the 5-gram bar. This works on the basis that many precious metal dealers have much larger inventories and can therefore offer fractional purchases. Therefore, a precious metal savings plan with fractional ownership is particularly useful if you want to pay relatively small amounts into the savings plan each month that are less than the value of the gold or silver bar you want.

$fraction$

Cost-Average-Effect: Profits also or just after falling prices

An essential part of the cost-average-effect is that the on average cheaper purchase prices have an effect especially when - at least in the meantime - the rates or prices also fall. In fact, it is precisely after prices have fallen that "profits" can be made, so that price declines in precious metals prove to be extremely helpful. The fall in the price of gold would therefore help you as a saver. Then, for the same monthly savings contribution, you would receive more gold bullion, or at least a larger share of fractional ownership.

Contrary to the widespread opinion - interim - price declines in gold or silver are therefore by no means annoying for regular saving within the precious metal savings plan due to the cost-average effect, but are actually pleasing. This presupposes however that it concerns only intermediate and temporary price declines, there is however from the principle a long-term upward trend. Thus, in the optimal case, the gold price or silver price should tend to rise for years, but in the meantime, there should always be (more significant) price declines. Exactly then the CAE can bring its strength fully to bear.

Is the cost-average effect always the better alternative?

Previously, we briefly indicated that the cost-averaging effect always occurs, but it is not automatically the better alternative in every case. Let's stay with the previous example: You have 10,000 euros at your disposal and are now considering whether to invest the amount in gold bars immediately or to divide it over the next 50 months with 200 euros each month. If you invest the 10,000 euros immediately at a fairly high or average gold price, the cost-average effect would probably be the better choice.

However, if you are lucky or skilled enough to purchase the bars at a fairly low price and the gold price only increases thereafter - except for small fluctuations - the CAE would be the worse alternative. So it depends on the point in time you buy and the subsequent development, if and to what extent you profit from the average cost effect.

Average cost effect increases total return

At the beginning of our article we briefly mentioned that the cost-average effect not only leads to cheaper buying prices, but even positively influences the total return. Why is this so? For this you need to know that the return of an investment or savings product is always composed of two components. On the one hand there is the yield or also the price increase (performance), which can be seen for example with gold or silver. These are in fact your earnings, which you achieve as an investor.

On the other hand, the returns are offset by the costs. With a precious metal savings plan, these can consist, for example, of administration or custody fees, the difference between the buying and selling price and, of course, the money you spend on the monthly savings installments. Exactly at this point costs can be saved by the cost-average-effect, as you can buy more shares of gold or silver or more bars from time to time for the same amount of Euros. By taking advantage of more favorable buying rates, you lower your costs and thereby automatically increase the return. Based on this principle, the total return is therefore somewhat higher due to the cost-average effect than if you buy, for example, two gold bars on a fixed monthly basis.

Calculating the cost-average effect with a real example

Now we have talked a lot theoretically about the cost-average effect, but now we would like to show with a practical example that it actually works. Due to the simpler representation we assume in the following example that you have invested in the past monthly for the equivalent of about 1,800 dollars or about 1,500 euros in a precious metal savings plan, because that corresponds approximately to the value of a fine ounce of gold.

What can you see in the following table? First, in the first column we present the real prices for the troy ounce of gold from September 1, 2011 to August 1, 2012. Why this period? Because this allows us to explain the previously explained cost-average effect well in the sense that it is precisely when gold prices are falling that "profits" can be made.

In the second column you can see how many 1-ounce gold bars with fractional ownership you would have bought in the respective month if you had paid the equivalent of $1,800 into the savings contract each month. The third column shows how many 1-ounce gold bars (also by fractional ownership) you would have held if you had purchased a fixed amount of one bar per month. The respective sum of the total holdings in connection with the respective capital investment then shows how many shares you would have more due to the cost-averaging effect or by how much the average purchase price is lower.

Date	Price fine ounce in dollars	Stock at purchase for 1,800 dollars	Purchase 1 bar Cost in USD
01.09.11	1.825,35	0,9861	1.825,35
03.10.11	1.660,95	1,0837	1.660,95
01.11.11	1.714,55	1,0498	1.714,55
01.12.11	1.745,40	1,0312	1.745,40
02.01.12	1.572,70	1,1445	1.572,70
01.02.12	1.745,50	1,0312	1.745,50
01.03.12	1.718,58	1,0473	1,718,58
02.04.12	1.678,85	1,0721	1.678,85
01.05.12	1.662,10	1,0829	1.662,10
01.06.12	1.626,05	1,1069	1.626,05
02.07.12	1.596,50	1,1274	1.596,50
01.08.12	1.600,10	1,1249	1.600,10
Total stock		12,888 Bars	12 bars
Capital investment		21.600 dollars	20.146,63 dollars
Average price		1.675.98 dollars	1.678.88 dollars

From the result of the comparison, you can see that the cost-average effect works. On the one hand, you have a higher total inventory when buying regularly for $1,800 per month, but you also had to invest more capital. On the other hand, if you buy a 1-ounce gold bar every month, your total holdings are lower, but you also had to put in less capital. What is decisive, however, is that you achieved a lower average purchase price in the first case.

Here, $1,675.98 in regular savings at $1,800 per month compares to an average rate of $1,678.88 if you had bought a bar on a fixed monthly basis. So we are talking about a difference of $2.90. Extrapolated to a stock of 12,888 bars, that would be a cost savings of about $37. This may not sound like much, but of course it is only the result of saving for one year. On the other hand, the savings is certainly not as great as many investors would think, because measured against the capital investment of $21,600, it is "only" about 0.17 percent.

So the result reveals the following facts:

The cost-average effect works
You save about 37 dollars in costs in the exemplary year
However, the CAE does not lead to a particularly large saving in relation to the capital investment

How big is the cost-averaging effect really?

How big the cost-averaging effect really is is not at all undisputed. Some experts praise the cost-averaging effect to the skies, while other experts are more moderate in this regard. The fact is that the effect of the CAE leads to ever greater savings (expressed in euros) with increasing savings duration. However, the effect is certainly not as large in nominal terms as many investors or savers would expect. This is also shown by our previous example. However, if you are faced with the decision to buy, for example, a 5-gram gold bar on a fixed monthly basis or to buy gold for a fixed 1,000 euros per month, everything speaks for the second and nothing for the first variant.

Further information based on the cost-average effect

Multiple award-winning gold savings plan
Our savings plan calculator

Was ist der Cost-Average-Effekt? Einfach erklärt

Table of Contents